What is a Straight Line in Mathematics?

Introduction:

The concept of What is a straight line in Mathematics? is foundational. It is one of the simplest and most fundamental geometric shapes, yet its implications and applications are vast and profound. In this article I will try to explain into the concept of what is a Straight Line in Mathematics, exploring its definition, properties, equations, and significance in various mathematical contexts.

Explanation:

Definition of a Straight Line:

In geometry What is a Straight Line? is an infinite set of points which can be extended in both directions without any curvature. It has no thickness, no width, and no height; it is one-dimensional. The straight line is often considered the shortest distance between two points, a concept that is both intuitive and mathematically rigorous.

Historical Perspective:

The study of straight lines dates back to ancient civilizations. Euclid, a Greek mathematician, provided a systematic study of geometry in his work "Elements," where he defined a straight line as "a line which lies evenly with the points on itself." This definition, though simple, encapsulates the essence of straightness—consistency and uniformity in direction.

Basic Properties of a Straight Line:

1. Linearity

A straight line is characterized by its linearity, meaning it does not curve or bend. This property can be observed by plotting the line on a Cartesian plane, where it appears as a continuous line extending infinitely in both directions.

2. Infinite Length:

A straight line can be extended infinitely in both directions. This infinite nature is a key property that distinguishes lines from line segments, which have defined endpoints, and rays, which extend infinitely in only one direction.

3. No Thickness:

A straight line is one-dimensional. It has no thickness or width, making it an idealized geometric object. In practical terms, when we draw a line on paper, it will have some thickness, but mathematically, a line is considered to have zero width.

Equations of a Straight Line:

The representation of straight lines using equations allows for a precise mathematical description. There are several forms of the equation of a straight line, each with its own advantages depending on the context.

a. Slope-Intercept Form:

The slope-intercept form is one of the most commonly used equations of a straight line. It is given by:

y= mx+c

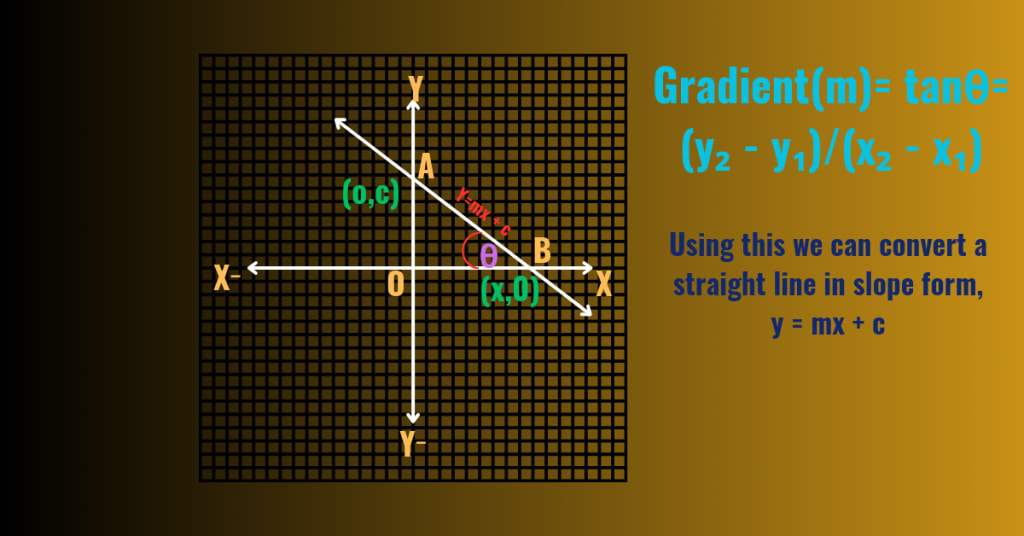
where m represents the slope or gradient of the line, Again m can be expressed as,

m = tanθ = (y₂ - y₁) / ( x₂- x₁),where θ = Inclination of the straight line,and(x₁,y₁), (x₂,y₂) are two points passes through the straight line.

and c represents the y-intercept. The slope m measures the steepness of the line, defined as the ratio of the rise (change in y) to the run (change in x). The y-intercept c is the point where the line crosses the y-axis.

For example, if we have the equation y = 2x+3, the slope(m) is 2, and the y-intercept(c) is 3. This means the line rises 2 units for every 1 unit it moves to the right, and it crosses the y-axis at the point (0, 3).

Some Problems related on Slope Intercept form of Straight line:

Question(1): The y-intercept and slope of a line is 5 and -1 respectively.Find the equation of the line.

Solution: y-intercept(c) = 5

Slope of the line (m) = - 1

∴ Equation of the line,

y = mx + c

=> y = (-1)x + 5

=> y = - x + 5

=> x + y = 5

Question(2): If (2,3) and (-1,1) points lie on a straight line, find the slope of the line.

Solution: ∵ x₁ = 2, y₁ = 3

x₂ = -1, y₂ = 1

∴ Slope of the line (m) = ( y₂ - y₁) /( x₂ - x₁)

= (1 - 3) /(-1 - 2)[putting values]

= - 2/ -3

= ⅔

b. Point-Slope Form:

The point-slope form is useful when we know a point on the line and its slope. It is given by:

y−y₁= m (x - x₁)

where (x₁,y₁) is a known point on the line, and m is the slope of the line.

For instance, if we know a line passes through the point (2, 3) with a slope of 4, the equation is:

y−3=4(x−2)

This can be simplified to the slope-intercept form if needed.

c. Standard Form:

The standard form of the equation of a linear straight line is:

Ax+By=C

where A, B, and C are constants. This form is particularly useful in solving systems of linear equations and in integer arithmetic.

For example, the equation 3x+4y=12

represents a straight line. We can convert this to the slope-intercept form to find the slope and y-intercept:

As we have,

3x+4y=12

=> 4y = - 3x + 12

=> y = - ¾ x + 12/4

=> y = - ¾ x + 3

So, the slope of the straight line is −3/4 and the y-intercept is 3.

Some Problems related on Straight line:

Question(a):Find the slope and y-intercept of the given line, - x + 10 = 5y

Solution: ∵ - x + 10 = 5y

=> y = - x /5 +10/5

=> y = - ⅕ x + 2

now comparing the above equation with y = mx + c

we get,

Slope (m) = - ⅕

and y-intercept (c) = 2

Question(b):Gradient of a line is 2 and passes through the point (-3,1),find the equation of the straight line.

Solution: ∵ Gradient of the line(m) = 2

point = (-3,1)

∴ Equation of the straight line,

y - y₁ = m(x - x₁)

=> y - 1 = 2{x - (-3)} [putting values]

=> y - 1 = 2 ( x + 3)

=> y - 1 = 2x + 6

=> - 2x + y -1- 6 = 0

=> - 2x + y - 7 = 0, which is the required equation of the straight line.

Question(c): The gradient of a straight line is -1 and y-intercept is 3, find the equation of the straight line.

Answer: Gradient (m) = - 1

y-intercept (c) = 3

∴ Equation of the straight line will be,

y = mx + c

=> y = (- 1)x + 3 [ putting value]

=> y = - x + 3

Graphical Representation:

Graphing a straight line involves plotting points that satisfy the line's equation and connecting them with a continuous line. The graphical representation provides a visual understanding of the line's behavior and properties.

1. Plotting Points:

To graph a line, we can start by choosing values for x and calculating the corresponding y values using the line's equation. Plotting these points on a Cartesian plane and connecting them gives us the line.

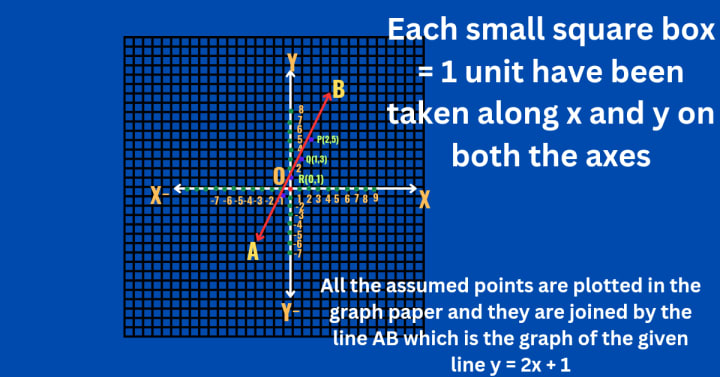
For example, for the line y=2x+1,

we can choose x values such as -1, 0, 1, and 2, and find the corresponding y values:

When x=−1,then from above equation we get, y=2(−1)+1 = - 2 + 1 =−1

When x=0,then from above equation we get, y=2(0)+1= 0 + 1 =1

When x=1,then from above equation we get, y=2(1)+1 = 2 + 1 =3

When x=2,then from above equation we get, y=2(2)+1= 4 + 1 =5

Plotting these points and connecting them gives us the graph of the line.

2. Using Intercepts:

Another method is to use the x-intercept and y-intercept. The x-intercept is the point where the line crosses the x-axis, and the y-intercept is the point where the line crosses the y-axis.

The Intercept form of a straight line is ,

x/a + y/b = 1,

where, a = x-intercept

b = y-intercept

For example,Find x and y intercept of the line 3x+4y=12

Solution:To find the x-intercept,we will take y=0

now the equation will become

3x+4(0)=12

=>3x + 0 = 12

=>3x =12

=>x= 12/3

=>x = 4

So, the x-intercept is 4

To find the y-intercept,we will take x=0,now the equation will become,

3(0)+4y=12

=>0 + 4y = 12

=>4y=12

=>y=12/4

=>y = 3

So, the y-intercept is 3

The above sum can be done in another way also,

∵ 3x+4y=12

=> 3x /12 + 4y / 12 = 12 / 12 [dividing bothsides by 12]

=> x/4 + y/3 =1 [Converting the given equation similar to x/a + y/b = 1]

∴ The x-intercept is 4

and the y-intercept is 3

Plotting these intercepts and connecting them gives us the graph of the line.

Some Problems related on Intercept of straight line:

Question(A):The x-intercept and y-intercept of a straight line are 2 and 3 respectively,find the equation of the straight line.

Solution: x-intercept(a) = 2

y-intercept(b) = 3

As we know that intercept form of a straight line is,

x / a + y / b = 1

=> x / 2 + y / 3 = 1 [putting values]

=> 6(x / 2 + y / 3) = 1X 6 [ As L.C.M of 2 and 3 is 6,so multiplying bothsides by 6]

=> 3x + 2y = 6, which is the required equation of the straight line.

Question(B): Find x-intercept and y-intercept of the given straight line, 3x - y = 12

Solution: ∵ 3x - y = 12

=> 3x /12 - y/12 = 12/12

=> x / 4 + y / (-12) = 1

Now comparing the above equation with x/a + y/b = 1 we get,

x-intercept(a) = 4

and y-intercept(b) = -12

Slope of a Straight Line:

The slope of a straight line is a measure of its steepness and direction. It is a crucial concept in understanding the behavior of lines.

1. Definition of Slope:

The slope m of a line passing through two points (x₁,y₁) and (x₂,y₂) is given by:

m=(y₂- y₁) / (x₂- x₁)

This formula calculates the rate of change of y with respect to x.

2. Positive and Negative Slope:

A positive slope indicates that the line rises as x increases. For example, the line y=2x+1 has a positive slope of 2, meaning it rises 2 units for every 1 unit it moves to the right.

A negative slope indicates that the line falls as x increases. For example, the line y=−3x+4 has a negative slope of -3, meaning it falls 3 units for every 1 unit it moves to the right.

3. Zero and Undefined Slope:

A zero slope indicates a horizontal line, where y remains constant regardless of x. For example, the line y=5 is horizontal.

An undefined slope indicates a vertical line, where x remains constant regardless of y. For example, the line x=2 is vertical.

Parallel and Perpendicular Lines:

Now, we will understand the relationships between lines involve in studying parallel and perpendicular lines.

1. Parallel Lines:

Two lines are parallel if they have the same slope but different y-intercepts. Parallel lines never intersect.

For example, the lines y=2x+1 and y=2x−3 are parallel because they both have a slope of 2.

Some Problems on Parallel Lines:

Question(x): Find a straight line which is parallel to the line 2x + 3y = - 1 and passes through the point (- 2, - 1)

Solution: 2x + 3y = - 1

=> 3y = - 2x - 1

=> y = - ⅔ x - ⅓ [dividing both sides by 3]

∴ gradient of the line (m₁) = - ⅔

∵ we will find a line which is parallel to the above line, then

m₂ = m₁ [ Let, m₂ is the gradient of the line which we will find]

=> m₂ = - ⅔

Now, we will find the line which passes through the point (-2,-1) and has gradient - ⅔ also parallel to 2x + 3y = - 1

∴ Required straight line will be,

y - y₁ = m (x - x₁)

=> y - (-1) = - ⅔ [x - (-2)]

=> y + 1 = - ⅔ ( x + 2)

=> 3(y + 1) = - 2 ( x + 2)

=> 3y + 3 = - 2x - 4

=> 2x + 3y + 3 + 4 = 0

=> 2x + 3y + 7 = 0

Question(y):Find the equation of straight lines which is parallel to x - 2y + 5 = 0 and at unit distance from the point (- 2, 2)

Solution: Let, the line parallel to x - 2y + 5 = 0 is x - 2y + c = 0

Now, the distance of the above line from the point = (Ax₁+ By₁+c) / ±√(A² + B²)

= [1(-2) +(-2)2 +c] / √(1)² +(-2)² [ Here,A = 1,B = - 2, x₁ = - 2 and y₁= 2]

= (- 2 - 4 + c) /±√1 +4

= (- 6 + c) /±√5

Now, according to question,

(- 6 + c) /±√5 = 1

=> - 6 + c = ±√5

=> c = 6 ±√5

∴ Required straight lines will be,

x - 2y + 6 +√5 = 0 [ putting value of c]

and x - 2y + 6 -√5 = 0 [ putting value of c]

2. Perpendicular Lines

Two lines are perpendicular if the product of their slopes is -1. This means the slopes are negative reciprocals of each other.

For example, if one line has a slope of ¾ then the slope of perpendicular line of it will be - 4/3

Some Problems on Perpendicular Lines:

Question(m): Find the equation of straight line which is perpendicular to the line 2x + 3y + 1 = 0 and passes through the point (2,1)

Solution: ∵ 2x + 3y + 1 = 0

=>3y = - 2x - 1

=> y = - ⅔ x - ⅓ [dividing both sides by 3]

∴ gradient of the line(m₁) = - ⅔

Let, the gradient of the line which is ⊥ to the given line = m₂

As, we know for two perpendicular lines,

m₁ X m₂ = -1

=> - ⅔ X m₂ = -1 [ putting value]

=> m₂ = 3/2

∴ Required equation of straight line will be

y - y₁ = m₂ ( x - x₁)

=> y - 1 = 3/2 ( x - 1)

=> 2y - 2 = 3x - 3

=> 3x - 2y - 3 +2 = 0

=> 3x - 2y - 1 = 0

Question(n): Check whether given pair of lines are perpendicular or parallel,

3x - y + 2 = 0

x + 3y -1 = 0

Solution : ∵ 3x - y + 2 = 0

=> y = 3x + 2

∴ Gradient of the line(m₁) = 3

Again, x + 3y -1 = 0

=> 3y = - x +1

=> y = - ⅓ x + ⅓ [dividing both sides by 3]

∴ Gradient of the line(m₂) = - ⅓

As, m₁ ≠ m₂

So, the given pair of lines are not parallel.

Again,

m₁ x m₂

= 3 x ( - ⅓)

= - 1

So, the given pair of lines are ⊥ to each other.

Applications of Straight Lines:

Straight lines have numerous applications in various fields, like geometry and algebra to physics and engineering.

1. Geometry:

In geometry, straight lines are used to define shapes, angles, and other geometric figures. They form the basis for understanding more complex geometric concepts.

2. Algebra:

In algebra, straight lines are used to represent linear equations and inequalities. They give a visual way to understand solutions to equations and systems of equations.

3. Calculus:

In calculus, straight lines are used to approximate curves through the concept of tangent lines. The slope of a tangent line to a curve at a point represents the instantaneous rate of change of the function at that point.

4. Physics:

In physics, straight lines are used to model motion and forces. For example, the motion of an object with constant velocity is represented by a straight line on a position-time graph.

To Read more...